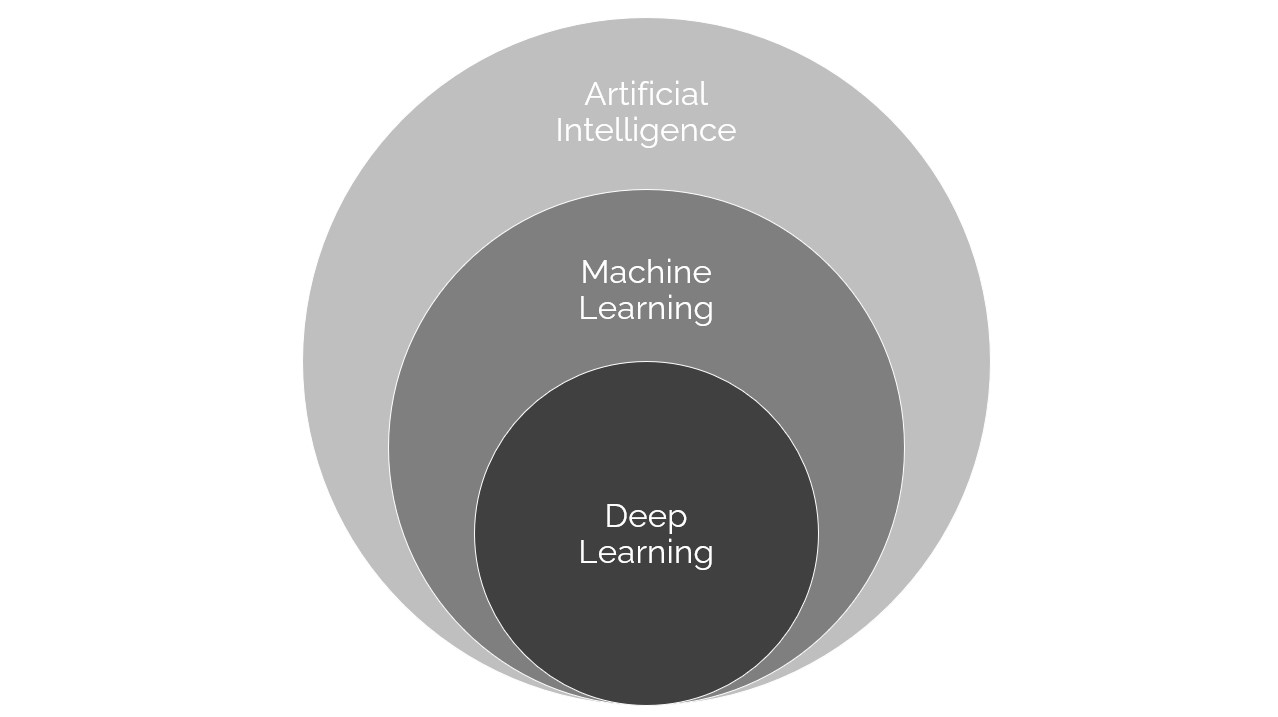
자연어 처리(Natural Language Processing) 와 딥러닝(Deep Learning) 알고리즘
최근 자연어 처리(Natural Language Processing) 분야는 신경망 기반 딥러닝(Deep Learning) 알고리즘을 적용하여 성능이 비약적으로 개선되었다. 문맥 기반(context-based) 시퀀셜 데이터(sequential data) 분석을 지원하는 순환신경망(RNN), LSTM, 나아가 현재 각광받고 있는 Bert, GPT 기계 번역 모델의 기반이 되는 Transformer 알고리즘 등이 모두 신경망 구조를 갖고 있다.
1. 딥러닝(Deep Learning) 알고리즘이란
딥러닝(Deep Learning)은 머신 러닝(Machine Learning)의 일종이고, 일반적인 머신 러닝 알고리즘과 달리 신경망 (Neural Networks) 구조를 취하는 머신 러닝 알고리즘을 딥러닝 알고리즘이라고 부른다. 비용함수를 계산하는 방법은 기존 머신 러닝 방법과 딥러닝 방법이 유사하지만, 신경망 구조의 여부에 따라 수학적 모델 및 학습 방법에서 차이가 나타난다.
특히 자연어 데이터와 같은 비정형 데이터에 대해 일반적인 머신러닝 알고리즘보다 성능이 높게 나타나는 특징이 있어, 자연어 처리(NLP)에 딥러닝을 접목하여 자연어 처리 성능을 높이는 방법이 자주 활용되고 있다.
2. 신경망 (Neural Networks)
신경망 구조를 간단하게 도식화하면 아래 그림과 같다. 입력층(Input Layer), 은닉층(Hidden Layer), 출력층(Output Layer)을 갖는 기본 구조를 가지고 있다.
[그림 1] 신경망의 구조 예
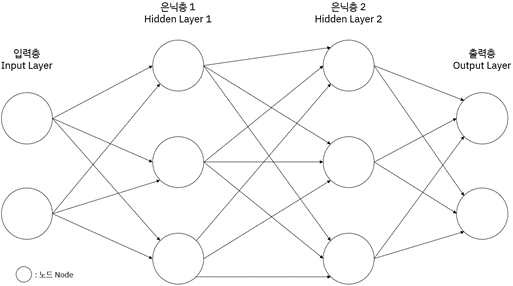
입력층과 출력층은 항상 단일층으로 구성된다. 은닉층의 수는 1개 이상이어야 한다. 단일층으로 구성할 수도 있고, 여러 층으로 구성할 수도 있다. 은닉층의 수는 데이터와 태스크의 종류, 성능기대치에 따라 사용자가 결정한다. 이때 은닉층이 2개 이상인 경우를 다층 신경망(deep neural networks), 또는 딥러닝(deep learning) 알고리즘이라고 부른다. 단일한 은닉층을 가진 신경망은 얕은 신경망(shallow neural networks)이라고 칭한다.
2.1. 각 층(Layer)의 역할
입력층(Input Layer)은 각 관측치에 대해서 피쳐값(features), 즉 독립변수에 대한 값이 입력되는 층이다. 피쳐값을 입력 받고 다음 층인 은닉층으로 정보를 전달한다.
은닉층(Hidden Layer)은 입력 받은 데이터에서 종속변수의 값을 예측하는데 긴요한 변수의 특성들을 추출한다. 출력층(Output Layer)은 종속변수의 예측값을 출력한다.
2.2. 각 노드(Node)의 역할
각 층(layer)은 여러 개의 노드(nodes)로 구성되어 있다. 노드들은 신호 또는 정보를 입출력해주는 역할을 한다. 노드(node)를 인간의 신경 전달 물질에 빗대어 뉴런(neuron) 또는 인공 뉴런이라고도 부른다. 이 때 다수의 신호를 입력 받아 하나의 신호를 출력하는 하나의 구조를 단순 퍼셉트론(single-layer perceptron) 알고리즘이라고 한다. 신경망(neural networks) 구조는 여러 다발의 퍼셉트론(perceptron)을 조합한 형태를 띤다.
각 노드의 역할을 이해하기 위해 독립 변수(Individual variable)가 2개(X1, X2), 은닉층 1개, 은닉 노드가 2개(H1, H2), 출력 노드가 1개(O1)인 간단한 회귀 문제 모델 A를 가정해보자. 회귀문제에서 종속변수(Dependent variable)가 가질 수 있는 값은 1개이므로 출력층에 출력 노드가 1개(O1) 존재한다. 이 모델은 은닉층이 단일하므로 다층 구조를 가진 딥러닝 구조기보다는 단순한 형태의 얕은 신경망(shallow neural networks) 모델이다.
입력층(Input Layer)의 노드의 수는 독립 변수의 수만큼 존재한다. 입력층의 입력 노드는 입력된 값 (독립변수 또는 피쳐값)을 은닉층으로 전달한다. 이때 편향 노드(b; bias node)는 값을 입력 받지 않는다.
| *편향 노드 (b; bias node)란: 선형회귀모델 y=ax+b 에서 y절편 (y-intercept) b 에 대응하는 개념이다. 바이어스(bias)라고도 부른다. 1을 값으로 출력한다. 입력층, 은닉층에 존재할 수 있다. |
위에서 가정한 신경망 모델 A에서 독립변수 X1, X2에 대해 입력 노드 I1은 X1의 값을 입력 받고, 입력 노드 I2가 X2의 값을 입력 받아 은닉층으로 전달한다. 입력층에 활성화 함수가 존재하는 경우 활성화 함수를 통해 신호를 변환하여 은닉층에 전달한다.
은닉층의 노드의 수는 성능기대치, 태스크의 종류, 데이터의 특성 등을 고려하여 사용자가 결정한다. 입력층에서와 마찬가지로 은닉층에 활성화 함수가 존재하는 경우 활성화 함수를 통해 입력 받은 신호를 변환하여 다음 층에 전달한다. 같은 층에 있는 노드 간에는 같은 활성화 함수를 사용한다. 모델 A에서 은닉층의 활성화 함수를 f(h) 라고 하자.
은닉 노드 H1에 입력되는 값은 입력층에서 전달한 신호의 가중합(weighted sum)이다.
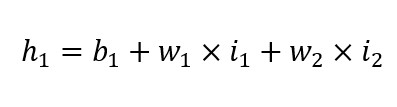
| *가중합(weighted sum)이란: 가중합이란 각 노드의 입력값에 노드가 갖는 가중치(w; weight) 를 곱한 값을 모두 더하고 바이어스(b) 값을 더한 값이다. 이때 가중치(weight)는 선형회귀모델 y=ax+b 에서 기울기 a 에 대응하는 개념이다. 통상 딥러닝 알고리즘에서는 파라미터(parameter)를 가중치(weight)로 표현한다. |
출력층의 노드의 수는 회귀문제(Regression)인지, 분류문제(Classification)인지, 문제의 종류에 따라 달라진다. 회귀문제라면 출력 노드의 수는 1개(O1)이다.
회귀 문제 모델 A에서 출력 노드 O1이 입력 받는 값(o1)은 은닉층에서 전달한 신호의 가중합이다.
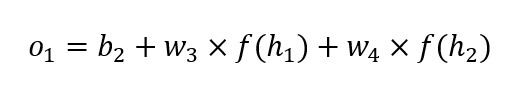
출력층에 활성화 함수의 유무는 문제의 종류에 따라 다르다. 회귀 문제의 경우 출력층에 활성화 함수가 없으며, 출력값 f(o1)이 항등식을 따른다. 즉 f(o1)=o1 이고, 출력 값이 종속변수의 예측치 (y)이므로 y = o1 이다.
모델 A에서 종속변수에 대한 예측치는 다음과 같이 구한다.
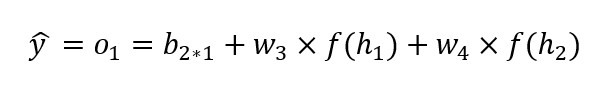
회귀 문제는 주로 평균제곱오차(Mean Squared Error)를 이용해서 비용함수를 계산하고 모델 성능을 평가한다.
| *평균제곱오차(MSE; Mean Squared Error)란: 평균제곱오차(MSE)는 예측치의 정확성을 측정하는 방법이다. 오차의 제곱에 평균을 취한 값인 MSE가 작을수록 원본에 대해 예측치의 정확성이 높다. 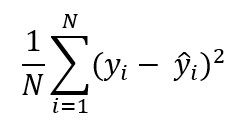 |
분류 문제 (Classification)인 경우 종속변수가 취할 수 있는 값에 대한 각각의 확률을 계산하는 함수식을 사용한다. 출력 노드의 수는 종속변수(𝑦)가 취할 수 있는 값의 수이고, 각 노드가 출력하는 값은 종속변수가 특정 값을 가질 확률이다. 예를 들어 주어진 데이터가 A에 해당하는지 아닌지를 판단하는 문제인 경우 𝑦∈{0, 1}, 출력 노드의 수는 2개이다. 각 출력 노드가 출력하는 값은 𝑦가 각 값을 취할 확률 py=0, p(y=1)이다. 분류문제는 주로 교차 엔트로피(cross entropy)를 이용하여 비용함수를 계산하고 성능을 평가한다.
| *교차 엔트로피(Cross Entropy): 예컨대 종속변수가 취할 수 있는 값이 0또는 1일 때, 교차 엔트로피는 다음과 같이 구한다. 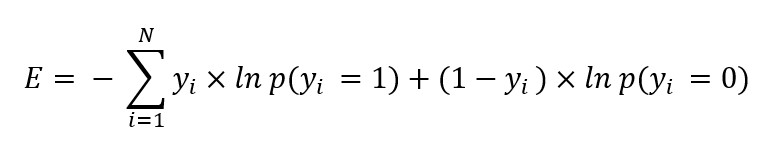 |
2.3. 활성화 함수(Activation function)
활성화 함수는 신경망 모델에서 입력 신호의 가중합(weighted sum)을 출력 신호로 변환하여 주는 함수다. 활성화 함수는 독립변수(Individual variable)와 종속변수(Dependent variable) 간의 비선형 관계를 표현한다. 이 함수는 특정 노드가 종속 변수 값을 예측하는데 미치는 영향(기여도)을 반영한다. 예측치에 더 많이 기여할수록 통상 더 큰 값이 출력된다.
| *활성화 함수 예: – Sigmoid Function (Logistic Function) – Hyperbolic Tangent Function (Tanh) – Rectified Linear Unit Function (Relu) – Leaky Rectified Linear Unit Function (Leaky Relu) – Exponential Linear Unit Function (Elu) |
2.4. 최적화 문제 (Optimization Problem)
비용함수(cost function)를 최소화하는 최적의 파라미터(parameter) 값을 찾는 문제를 최적화 문제(Optimization Problem)라고 한다.
딥러닝 모델에서는 경사하강법(Gradient Descent)을 사용하여 최적의 가중치를 구한다. 경사하강법이란 가중치(파라미터)의 값을 계속해서 바꾸어 가면서(업데이트 하면서) 비용함수의 값을 줄이는 가중치 값을 찾아가는 방법이다. 이때 사용하는 수식은 다음과 같은 형태이다.
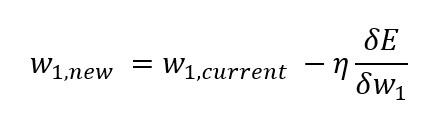
일반적으로 딥러닝 알고리즘의 비용함수는 볼록(convex)한 형태가 아니고 좀 더 복잡하며, 파라미터가 매우 많이 존재한다.
2.5. 경사하강법(Gradient Descent)
가중치를 업데이트할 때 사용하는 데이터의 양(volume)에 따라 경사하강법(Gradient Descent)에는 크게 3가지 방법이 있다.
| Gradient Descent | Number of data points | 개요 |
| Batch Gradient Descent | N | 가중치 업데이트를 할 때 전체 데이터를 모두 사용한다. |
| Mini-batch Gradient Descent | x;1<x<N | 한번 업데이트할 때 일부 데이터를 사용하고, 그 다음 업데이트에 또다른 일부 데이터를 사용한다. 이때 사용하는 일부 데이터를 ‘mini-batch’라 한다. |
| Stochastic Gradient Descent(SGD) | 1 | 무작위로 하나의 데이터 포인트를 선택하여 사용한다. |
2.6. 경사 하강 최적화 알고리즘 (Gradient Descendent optimization algorithms)
경사 하강 최적화 알고리즘 (Gradient Descendent optimization algorithms)는 경사하강법(Gradient Descendent)을 적용해서 비용함수 값을 최소화하는 가중치(weight) 를 찾는 역할을 하는 도구를 말한다. 최적화 도구(Optimizer)라고도 한다. 딥러닝 모델은 보통 파라미터가 매우 많고 안장점(saddle point)이 다수 관찰되며, 학습속도가 상대적으로 느리기 때문에 이를 개선, 보완하는 여러 최적화 도구가 고안되었다. 일례로 Adaptive Gradient(Adagrad), Adam, Adadelta, Momentum, Nesterov Accelerated Gradient(NAG), Root Mean Square Propagation(RMSprop) 등이 있다.
| *안장점(saddle point):안장점이란 3차원 공간의 곡면, 또는 다변수함수의 그래프 상에 나타나는 것으로, 보는 방향에 따라 극대값이 되기도 하고 극소값이 되기도 하는 점을 말한다. |
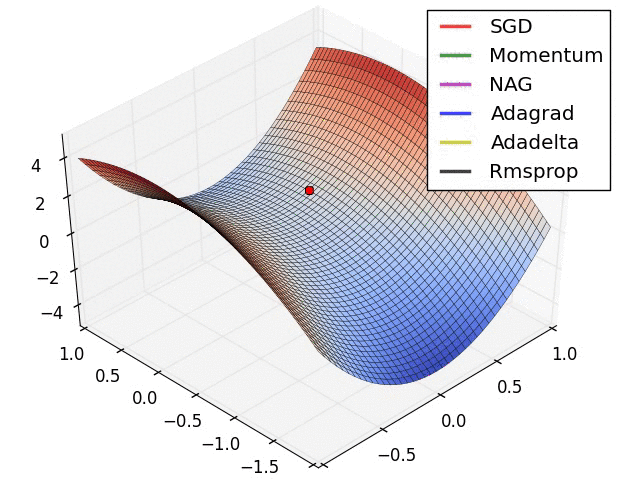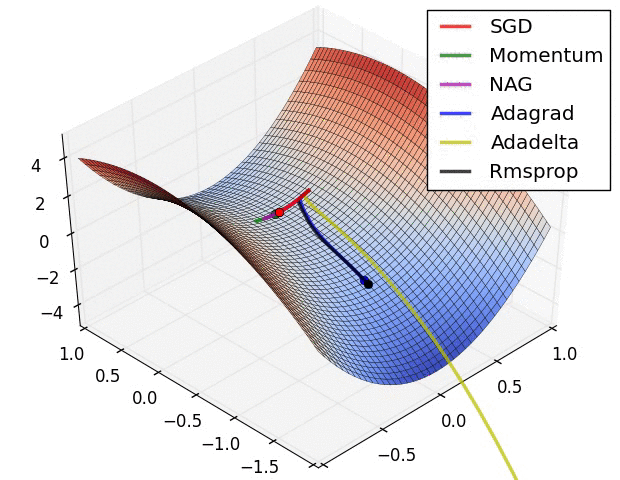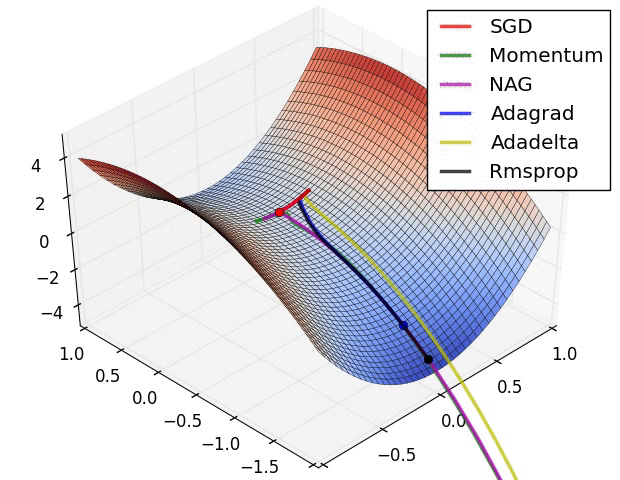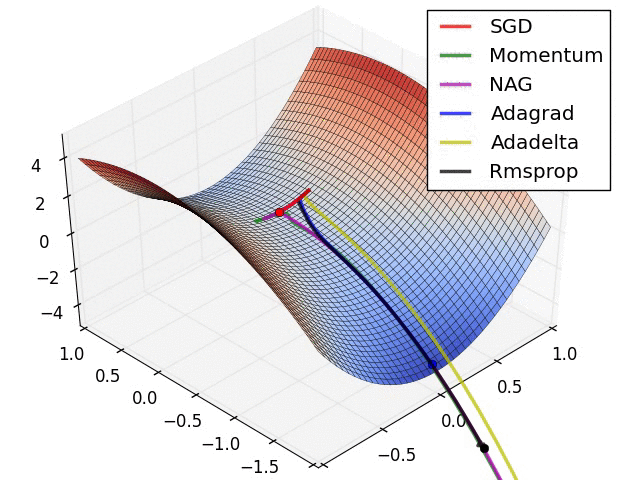
안장점 문제에서 SGD (Stochastic Gradient Descent) 알고리즘 별 최적화 동작을 시각화한 아래 그림을 참고하면, Adagrad, Adadelta, Rmsprop 등은 안장점을 벗어나서 최적화 방향으로 수렴하는 것을 볼 수 있다.
[그림 2] 안장점에서의 SGD 최적화 동작
3. 딥러닝과 지도학습(supervised learning)
신경망(neural networks)기반 딥러닝 모델은 지도학습(supervised learning) 문제 유형에 많이 사용된다. 이때의 지도학습 방법은 여타 기계학습(Machine Learning) 방법과 크게 다르지 않다. 우선 정답이 존재하는 데이터를 학습 데이터(training data)와 평가 데이터(test data; validation data)로 분리하고, 학습 데이터에서 독립변수와 종속변수 간 관계를 도출하며 비용함수를 최소화하는 최적의 파라미터(또는 가중치)값을 구한다. 이 값을 대입해 구체적인 모델을 만든다. 이 모델을 평가데이터(test data; validation data)에 적용해 모델의 정확성, 성능을 테스트한다. 테스트를 거쳐 만든 모델을 실제 풀고자 하는 문제에 적용해서 사용자가 알고자 하는 값인 예측치를 출력한다.
[참고 학습 자료]
– The Stanford Natural Language Processing Group, https://nlp.stanford.edu/
– Stanford University, CS224N: Natural Language Processing with Deep Learning, Winter 2019, Lecture 1-22, on Youtube, https://www.youtube.com/playlist?list=PLoROMvodv4rOhcuXMZkNm7j3fVwBBY42z
– Kyunghyun Cho, https://sites.google.com/site/deepernn/home/blog/lecturenotebriefintroductiontomachinelearningwithoutdeeplearning
– Kyunghyun Cho, https://github.com/nyu-dl/Intro_to_ML_Lecture_Note
[참고 문헌]
[1] 사이토 고키, 밑바닥부터 시작하는 딥러닝 (Deep Learning from Scratch), 한빛미디어, 2016 ; Saito Goki, Deep Learning from Scratch, O’Reilly, 2016
[2] 사이토 고키, 밑바닥부터 시작하는 딥러닝 2, 한빛미디어, 2019; Saito Goki, Deep Learning from Scratch 2, O’Reilly, 2018
*해당 콘텐츠는 저작권법에 의해 보호받는 저작물입니다.
*해당 콘텐츠는 사전 동의없이 2차 가공 및 영리적인 이용을 금하고 있습니다.